Construction of Circumcircle and Incircle

In the construction of orthocentre to the triangle, the following steps are to be followed

• Find the perpendicular from any two vertices to the opposite sides.
• To draw the perpendicular or the altitude, use vertex C as the center and radius equal to the side BC. Draw arcs on the opposite sides AB and AC.
• ?
• Similarly, draw intersecting arcs from points C and E, at G. Join BG.
• CF and BG are altitudes or perpendiculars for the sides AB and AC respectively.
• The intersection point of any two altitudes of a triangle gives the orthocenter.
• Thus, find the point of intersection of the two altitudes.
• At that point, H is referred to as the orthocenter of the triangle.

In the construction of orthocentre to the triangle, the following steps are to be followed

P- Observe the intersection of the perpendiculars.

Q- Draw the triangle, where you have to construct the orthocentre

R- Draw the perpendiculars from any of vertex to opposite side.

S- The point of intersection of perpendiculars is called orthocentre

T- Draw another perpendicular from another vertex.

Observe the correct sequence of the steps of construction.

Incentre is a

The point $"I"$ of the given triangle $ABC$ is

The point of intersection of the angle bisectors of a triangle is

The point $"H"$ in the given triangle $ABC$ is

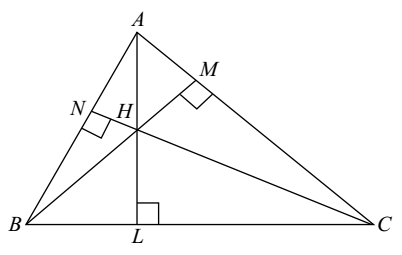
Orthocentre is a

The point of intersection of the altitudes of a triangle is

The orthocenter of a right-angled triangle is formed

The orthocentre of an acute angled triangle is

The orthocentre of an obtuse angled triangle is

The point equidistant from the three sides of a triangle is

The orthocentre of a triangle is determined by

The incentre of a triangle is determined by

The point where three altitudes of triangle intersect is known as

Point of intersection of angular bisector of a triangle is known as

In a triangle $XYZ$, $XY+YZ+ZX=14 \mathrm{cm}$ and $XY:YZ:ZX=4:2:4$. Construct the circumcircle of the triangle.

Draw a triangle with sides $x, x+1, x+2$ and perimeter$=18 \mathrm{cm}$. Draw its incircle. Measure and write the radius of the incircle.

Draw a circle of radius $3 \mathrm{cm}$. Draw triangle $ABC$ with this circle as circumcircle and angle $50°, 60°$ and $70°$.

Construct a regular pentagon in a circle of diameter $8 \mathrm{cm}$.